English
Every day we offer FREE licensed software you’d have to buy otherwise.

$39.00
EXPIRED
Giveaway of the day — Process Lasso Pro 8.9.8
Process Lasso will dynamically boost the performance of your PC.
$39.00
EXPIRED
User rating:
198
55 comments
Process Lasso Pro 8.9.8 was available as a giveaway on August 2, 2016!
Today Giveaway of the Day
Control remote desktop or laptop from any device and anywhere!
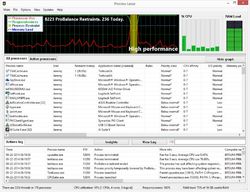
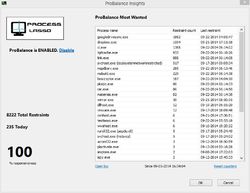
Process Lasso is NOT yet another task manager. It instead contains a fleet of algorithms designed to dynamically boost the performance of your PC. Among them is our famous ProBalance algorithm, which temporarily reduces the priority of troublesome background processes in order to improve PC responsiveness, as shown in real-world and synthetic tests. Further, the user can automate all kinds of system settings with rules and persistent process priorities, CPU affinities, etc..
What’s New:
- Substantial optimization of the core process management library Lasso uses;
- Several interoperability improvements;
- Localization improvements;
- Bug fixes.
System Requirements:
Windows XP/ Vista/ 7/ 8/ 10
Publisher:
Bitsum TechnologiesHomepage:
https://bitsum.com/File Size:
7.3 MB
Price:
$39.00
How would you improve Process Lasso Pro 8.9.8?
Comments on Process Lasso Pro 8.9.8
Thank you for voting!
Please add a comment explaining the reason behind your vote.
Please add a comment explaining the reason behind your vote.
You can also add comment viaFacebook
Facebook comments
iPhone app giveaways »
$19.95 ➞ free today
$0.99 ➞ free today
Every Day Spirit is a collection of beautiful, original, hand-crafted wallpapers created to make your phone look amazing.
$0.99 ➞ free today
$4.99 ➞ free today
$1.99 ➞ free today
Android app giveaways »
$0.99 ➞ free today
$0.99 ➞ free today
Spelling Right is a new challenging educational spelling game that will test your English spelling skills.
$2.29 ➞ free today
$0.99 ➞ free today
$1.49 ➞ free today



I have been waiting for over an hour to receive the License Code ...
It's not in my spam box, what give ?
Save | Cancel
My production machine is NOT connected to the internet (simplest Virus Protection). You can't register this application on a non-connected PC...
Other Software houses provide for off-line activation: Steinberg, Native Instruments, Adobe come to mind.
In it's current form the registration proccess is a fail for me. Deleted.
Save | Cancel
I've used an older version of Process Lasso Pro, and found it extremely helpful, especially when my system became slow. You can see with a click what processes are using up your memory, CPU time, etc. (okay, you can do this with Windows Task Manager, too).
But with Process Lasso Pro you can click on an unfamiliar process and it will tell you important information about it. If you see a process in the list that you don't recognize, click on it and it will tell you, for example, that it's being run by a program called "XYZ." If you didn't install XYZ and don't want it - it might have been something you tested awhile back, or that was snuck in on you when you installed something else - you can stop it and if you want, delete the program.
A great addition to my toolbox. Thanks GOTD and Process Lasso!
Save | Cancel
After praising GAOD and Bitsum (mfr. of Process Lasso Pro), I find that for the first time in many years of using GATD, I am having trouble installing. Someone else had the same problem, getting a message saying the installer integrity check has failed. I downloaded the zip file three times hoping for a clean installer, but no luck. It won't work to download the program from Bitsum, at least not to get PRO version free via GOTD. But with half off it's $30 for lifetime upgrades and updates, with licenses for every computer you own, I just may download it directly.
GOTD, get this fixed please! Windows 10 Home, 64 bit on a Lenovo Yoga 700.
Save | Cancel
Thank you for the program.
Am not using FB, so am posting my suggestion here.
Am a fairly savvy user. The number of selectable options and variables in the various menus is quite overwhelming.
Suggest that the number of the presented variable options and settings be selectable in 3 levels:
1. "Minimal".
2. "Intermediate", or "savvy".
3. "Advanced" or "expert".
BTW, Am still not sure whether using Process Lasso will be of advantage on an SSD centered PC (Win XP or Win7).
Would like to read about others experience.
Best,
Eldad
Save | Cancel
Oh,no! There was a problem with activation! It won't accept the activation code. Please advise.
Save | Cancel
This is actually a very useful program. To me it is one of the very best. I had to get another computer recently and this was the program I was missing but had forgotten all about it. So glad to have seen this today Thank You GAOTD and Bitsum. It would be a long time before I could buy anything I'm budgeting to survive not save and it looks gloomy for the rest of the year. So many goodies from GAOTD sometimes I feel like I've stumbled into Santa's Workshop so to help me not feel so guilty I do try to give feedback but I usually do it later with the developers of the programs. The thing is without GAOTD none of that would have been possible, so guys is there any way I can improve my side of the equation to help you back?
Save | Cancel
Well, you could try to say something more than useful program, one of the best, and I forgot about it.
Save | Cancel
I had this from gotd before and found it to be nothing but a space filler on my hd. If anything it slowed down my system and caused my games and videos to stutter. No thanks.
Save | Cancel
Mike OD, Task Manager does a reasonable job of letting you see what's using up your resources. If your system is creaking under the strain, simply shut down the unnecessary background tasks and tweak your startup programs .... Usually does the trick.
Save | Cancel
Lenny,
I am an average computer user, would you mind to name some examples of unnecessary background tasks?
Thank you for your kind response.
Regards,
consuella
Save | Cancel
Used to use this a few years ago on older kit where it did have a use but then found that with later equipment and OS's that it actually used up more resource than it is worth.
Using well known software to clean up junk and very useful utilities like Autorun organiser you can now easily get enough information about what things could be resource hogs and deal with them.
Process Lasso may well still be of use if you are really prepared to dig deep into it's features to eek the very last ounce of performance out of your PC but for most users it is just something that will sit in your system tray using up valuable resources with no really beneficial effect.
Save | Cancel
Still waiting on email with licence !
Save | Cancel
Ran this program on Windows 7 and it worked great. Kept everything tidy and did speed up performance.
Windows 10 has most of these features built in. It will probably interfere with the OS and slow things down.
Save | Cancel
Bought this years ago and love it. Just posting here to give props to this excellent utility.
Save | Cancel
Matt,
I second what Matt has to say. It has so much functionality that one could spend hours in discovery. I use it vanilla out of the box and get lots from it. 2 thumbs up!!
Save | Cancel
And I second what warpwiz has to say, thereby I suppose "thirding" what Matt says. I've been using Process Lasso (PL) for a number of years, and with a paid licence use it on multiple PCs.
I find PL to be very effective since at times I bombard my systems with lots of concurrent jobs, and as a "power user" it's very easy to configure PL to give some of those jobs higher or lower priorities (CPU cores used, processor affinity, etc).
PL generally helps even if don't tweak it and you just let it do its own thing, yet still I can imagine that for some other people's system workloads PL won't make much difference.
Save | Cancel
I have seen Windows crawl to a stop on its own but, NOTHING will slow things down like this one. It would have to be potty trained to let security software run at top priority. Since it sets itself as the A #1 priority, and bogs the sys down, its a shutdown for me. Uninstalled.
Save | Cancel
Keith, It won't be Process Lasso that is making your Windows crawl and it won't slow your computer down. You don't seem to know just how this program works and to blame Process Lasso just shows how little you know about Windows
Save | Cancel
I have been using this software for several years, back when I had a first generation EeePC running a very trimmed down Windows XP on a 600 MHz Atom processor (overclocked to 900 MHz). The first time I got it was as a free GAOTD, and oh, my! It optimized my Windows so much Firefox became able to smoothly play Flash videos, something it couldn't do before!
Afterwards, I won a Pro license in a promotion in the developer's Facebook page, and it has become one of the first utilities I install whenever I do a fresh Windows install or replace my computer, it is that amazing!
If you can, install this on every machine you have access to, it's well worth the effort. And then, purchase a license. This is one piece of software you won't ever regret having paid for!
Save | Cancel
Alexander Gieg, You are correct, it worked great on XP and 7, however there is no longer noticeable increase in performance on win 10 with 3GHZ processor. If you have 16GB DRAM installed, Lasso will not do any better than win 10 does, I've done the tests few months ago.
Save | Cancel
Kerry, I can believe there are non noticeable improvements in very powerful computers such as the one you describe. For less powerful ones however (my case) it still helps.
Here in Brazil computers are still very expensive. My home one is a six years old Core 2 Duo, and it was the second cheapest computer at the store even back then. In the meantime I managed to double its RAM to 8 GB and to add a bigger HDD, but that was it. So, for me and for those in a similar situation, Process Lasso is still useful. :-)
In 5 to 10 years, when my computer breaks down for good, I might not need it anymore. Until then however, I'm happy keeping it installed! :-D
Save | Cancel
"... however there is no longer noticeable increase in performance on win 10 with 3GHZ processor. If you have 16GB DRAM installed, Lasso will not do any better than win 10 does"
--
" For less powerful ones however (my case) it still helps."
If you spend much time watching 10's Task Mgr., you'll see 10 tends to have more processes going on in the background. In my experience it can make a very low powered CPU [e.g. an Atom] seem more powerful & make the system more responsive, *until* you do something really CPU intensive where it's true lack of power is revealed. OTOH running 10 on something like a i7 k, that habit can slow things down, as the system winds up waiting for several processes to finish doing their thing, so it can get down to applying it's full muscle to heavier workloads.
There's also a potential problem moving lots of data. Regardless the speed of your drive(s), & even with SSDs, a device can only move a certain amount of data at a more limited speed to & from the drive(s). Many processes can interrupt that data flow.
Process Lasso can help in both situations [and more], but the amount of help it provides varies -- it's more noticeable in some situations, depending on the task(s) & hardware, than in others. Running Process Lasso while I'm typing this using this PC does not provide a benefit that I can easily see. If I were editing a bunch of large RAW image files, or in a game where tweaking for every fps matters, that would be a different story. So I start & run Process Lasso when/where it can make a bigger difference, don't bother with it when it doesn't.
Save | Cancel
Kerry, You need to learn the options and how to use them after I tweaked the six cores in mine it act likes it can read my mind and start the programs I was about to click it's gotten so fast. I now feel my computer can keep up with my graphics card instead of bottle necking it. I can see the increase but I am using win 7 pro 64 bit. Don't know about Win 10, Good Luck and give it a try tweaking you can just reset when it doesn't do what you want it to do.
Save | Cancel
3 Thumbs Up from me -- I've been using Process Lasso for 3+ years, and I think it helps maintain optimal sysytem responsiveness in my older PCs. Not only that, the GUI CPU graph, process list and process monitor log are handy tools for monitoring what's going on inside your PC...
It's both easy to install with it's default settings, or you can go wild tweaking it with all sorts of arcane custom CPU core and power saving options. Read the documentation first or visit the forum if you want to see how much engineering the inventor Jeremy Collake put into this product:
How ProBalance Process Priority Optimization Works – Bitsum
https://bitsum.com/how-probalance-works/
Bitsum Community Forum - Index https://bitsum.com/forum/
P.S. You can also check the thumbs up percentages on previous GOTDs of this piece of code... it's usually among the highest of GOTD offerings. Full disclosure: I receive no remuneration for endorsing this product, but I have had many conversations with Jeremy about Process Lasso... ;-)
Save | Cancel
The type of work I do on a computer rarely puts a high load on my system.
Having said that I wouldn't be without this program; so useful troubleshooting when you have problems, it has really helped me in the past.
Really useful when you have boot speed problems as the program contains so much useful information such as creation time of a program.
As I said I wouldn't be without it, it's a goldmine of information that is well presented in a really stable program.
Save | Cancel
I have Process Lasso from a previous GotD. Do I need to reinstall it to keep the free licence? I'm currently on version 8.9.8.36.
Save | Cancel
Dave K,
The dev behind Process Lasso is great, and generous... usually your GOTD license is good for that version number, regardless how many sub-versions [or perhaps builds is a better word] there are.
That said, whenever it's on GOTD you can try updating Process Lasso in-program, & if it works you're golden, if it doesn't grab the GOTD & you're still golden.
Save | Cancel
Installed ok but jams up [not responding] if i try and interact with it.
win7home .toshiba satellite. quad core laptop.So i cant put the code in to make it full version or do anything with the prog.
Save | Cancel
I installed Process Lasso 8.1 back in the day, after being offered here in this site. I installed it on my already CPU limited Surface 3 with an x7-z8700 proccesor, and after weeks of use without any seeing any significant difference at all (other than the very high number of cpu "restraints" this program is doing) I stopped using this.
If anybody else got a significant improvement while using a similar processor I´d love to know how.
Cheers
Save | Cancel
Great software, but, is there any available solution to the known problem of MalwareBytes Anti-Ransomware Beta causes high CPU usage in ProcessLasso?
Both programs are valuable and its frustrating to know that until this issue will be solved by either of the companies, users will have to choose which of the programs to run, since running them simultaneously causes continuous high CPU usage.
Save | Cancel
I installed this awhile back as a Giveaway and am now on v. 8.9.8.24. Will installing today's pro version give me any advantage I don't already have?
Save | Cancel
seagrape,
The revision history is here:
bitsum[.]com/changes/processlasso/#latest
Save | Cancel
I have a new Dell Quad Core PC, I have made sure that Core parking is turned off and all the cores are at 100% all of the time, which apparently came from the factory setup that way. I also have 16GB's of ram which I rarely use over 7GB's.
I wanted to ask how this software could possibly made my PC any better than it is?
Save | Cancel
Adam, if your CPU is running in the hundred percent all the time you have major problem. This should not be. CPU running hundred percent of the time is going to overheat. That is can lead to massive failure on your computer.
I would think that no third-party software is going to solve your problem you need to contact Dell.
Save | Cancel
kc4cop, Thank you. I'm sorry my bad, I didn't explain that correctly. What I meant was that Core Parking is turned off, therefore all of my Cores are available upon need without being throttled, not running 100% all of the time.
I decided to give Process Lasso a try, I like some of the additional features it has, I find them very useful. Such as the Anti Sleep Anti display sleep settings, that's really nice because I like to use a screen saver sometimes and using the antisleep/display settings for specific apps I can watch a movie or video using my browser that I setup to use with it without my screen saver or PC Sleep interrupting while the browser is running, along with other programs I setup to use with it like my Media Player.
I like the always higher priority settings for specific programs, I find that it is helpful with some softwares that I use and gives them a quicker response.
Save | Cancel
Adam,
"Core Parking is turned off, therefore all of my Cores are available upon need without being throttled, not running 100% all of the time."
You don't mention any CPU info -- for Intel it's Turbo Boost I believe, & it reduces the clock speed on a per core basis when you don't need it. Many over clockers just increase the max boost speed, but many choose to just run a steady, max clock rate instead. If the cooling's adequate, running at top clock speed only hurts your electric bill. If you want, run the free, portable CPUID HWMonitor, once or always -- it can show you the watts used, along with the clock speed per core if you turn on the Turbo Boost feature in the bios.
This morning the top CPU utilization on this rig is 55%, the top power reading is 62.21W, the lowest reading is 5.6W, while the top temp is 50C, & the lowest 29C. So Turbo Boost has saved me $ both running the PC & the A/C.
That said, while I don't have a big problem with with any lag using Turbo Boost on this PC in the ways I use it, you might want to check out another app from Bitsum called Park Control, which deals just with that sort of thing.
"I decided to give Process Lasso a try, I like some of the additional features it has, I find them very useful. "
Cool
Save | Cancel
Process Lasso's ability to keep my computer awake for 1, 2, 4, 8, 12 hours or indefinitely is useful to me when doing lengthy downloads or backups. In addition, I value the ability occasionally to throttle one or more processes by lowering their priority. The program has kept itself up to date in the three years since I installed it.
Save | Cancel
kc4cop, Check your Windows update as I have read it has been causing what you describe while checking for updates
Save | Cancel
Downloaded and THOUGHT it installed, but the only file in "program files" is CHECK64.EX(20kb) I run a 32bit system, but surely this program runs on both 32/64 bit systems?
Save | Cancel
WHAT period of time is the program free before it expires, 1 year or ?.......
Save | Cancel
tommo39, this is non-expiring license for Process Lasso PRO , but ONLY FOR THIS PARTICULAR VERSION (8.9.8), perhaps some minor updates apply to it, but for sure when the new major version comes out, we will be not entitled to the free upgrade.
Having said that, I still recommend trying the software.
Save | Cancel
Rafal Stanilewicz, I installed this program many years ago as a GOTD giveaway and it continues to update regularly. Today i am on version 8.9.8 without doing a reinstallation.
Save | Cancel
After trying out a previous GOTD offering of Process Lasso a few years back I was so impressed with it that I bought it. If you've not given Process Lasso a go then now is your time.
Save | Cancel
I bought this program after it appeared on GOTD last winter, when it solved an annoying W10 problem I was having. I haven't regretted doing so, and I recommend it to any reasonably knowledgable user.
Save | Cancel
Thanks, I've been using Process Lasso for a couple of years. It's a great program.
Save | Cancel
I have been using a paid version of this software for 2 years now on 4 PC's here in the office!
It works quite well allowing me to do intensive rendering and other operations with out failures
that caused problems in the past! The continual upgrades means it just gets better all the time.
Tech support is fast friendly and efficient. I have even had a call back on one problem. It is a
must have for a power user!
Save | Cancel