English
Every day we offer FREE licensed software you’d have to buy otherwise.

$25.00
EXPIRED
Giveaway of the day — Cinch Audio Recorder 2.0.1
Record high quality music from Online Music Streaming Sites!
$25.00
EXPIRED
User rating:
65
94 comments
Cinch Audio Recorder 2.0.1 was available as a giveaway on March 1, 2017!
Today Giveaway of the Day
Control remote desktop or laptop from any device and anywhere!
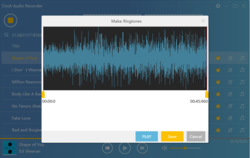
Cinch Audio Recorder is smart streaming music capturing tool that can save any music from online as mp3. If you are recording a playing list, music files will be saved on your computer separately. Also, you can cut part of a recorded music and save it as a ringtone for your phone.
System Requirements:
Windows XP/ Vista/ 7/ 8/ 10; Processor: 1 GHz Intel or AMD processor; RAM: 512 MB of RAM (1024 MB recommended); Disk Space: 1 GB of free hard disk space for typical installation of all components
Publisher:
Cinch SolutionsHomepage:
http://cinchsolution.com/File Size:
19 MB
Price:
$25.00
How would you improve Cinch Audio Recorder 2.0.1?
GIVEAWAY download basket
Developed by MPCSTAR
Developed by VSO Software
Store, manage and open media content from the cloud.
Developed by Online Media Technologies Ltd.
Comments on Cinch Audio Recorder 2.0.1
Thank you for voting!
Please add a comment explaining the reason behind your vote.
Please add a comment explaining the reason behind your vote.
You can also add comment viaFacebook
Facebook comments
iPhone app giveaways »
$19.95 ➞ free today
$0.99 ➞ free today
Every Day Spirit is a collection of beautiful, original, hand-crafted wallpapers created to make your phone look amazing.
$0.99 ➞ free today
$4.99 ➞ free today
$1.99 ➞ free today
Android app giveaways »
$0.99 ➞ free today
$0.99 ➞ free today
Spelling Right is a new challenging educational spelling game that will test your English spelling skills.
$2.29 ➞ free today
$0.99 ➞ free today
$1.49 ➞ free today


I can't register this product. When trying to register, it say's "Access server exceptionError #2032". Can anybody help me with this?
Save | Cancel
Eileen Joy · University of Michigan
Doesn't give info on bitrate. but when i checked, using windows, it seemed to be 116 or 114 for the songs i recorded. would have liked a little higher - at least 128, which is normal. Also, it played backmy internal computer dings - nowhere can I find a place to disable other sounds comng in. Finally, the playback button doesn't move, which shows you how many seconds you are into the song. Please can you tell me how to do these? I really don't want to record at anything under 128.
Save | Cancel
Nice program, but I have three issues with it:
(1) The audio quality is noticeably lower than the source files
(2) Songs are not recorded when I am playing songs via my USB headset
(3) Absolutely no data about the recorded songs is retrieved.
Save | Cancel
Henrik said, "That should not happen. We haven't received the similar issue reported by other users.".
as for my case, it is happen.
in 'About' says Version 1.0.2 not 2.0.1 as shown in the GOTD Giveaway.
but go to 'setting/check for updates', it says "u are using the latest version 2.0.1".
sorry, it is my 1st down in my life of using GOTD.
donald
Save | Cancel
donald,
Thank you for pointed out our mistake on version no. We will fix it for sure.
Save | Cancel
it would have been nice to try this programme, but all i get after downloading and unzipping it corrupt file, please download again, i think after 8 attempts at it and getting the same message every time is enough for me, never had a corrupt file from GAOTD before, shame looks like a good programme.
Save | Cancel
Popz,
It seems you have an issue with GOTD zip file. Please download it from our official site to see if you got the same issue.
Save | Cancel
.
Oops -- I played Windows Media Player to identify previously saved tracks WHILE I was downloading the next tracks from Pandora and recording with Chinch ...
... and of course Chinch recorded BOTH the incoming Pandora stream AND my Windows Media Player library on top of each other for a 29 minute mish-mash - trash.
So, no, no multi-tasking on ONE computer.
I suppose I can network another computer to see the Music directory on this computer and identify the songs as they land, without playing them through the came computer where Cinch is recording Pandora.
It would be nice, though, to record only the incoming stream, not the existing library playback via the other player, Windows Media Player.
.
Save | Cancel
We thought about it. But there is a technical limitation. The software record audio from the sound card, but it didn't tell us what the sound come from which program so, the software can make a decision which music/sound should be recorded or shouldn't.
Save | Cancel
.
[ Henrik ],
Twin sound cards ?
.
Save | Cancel
Thanks Henrik en GOTD! Nice program!
What I like to see in a future version:
- Possibility to record higher quality (by settings)
- Option to see or log the url from the (streamed) recordings
Save | Cancel
Like another user that installed on an XP SP3 OS, attempting to start the program, I get a dialog displaying:
"LCMapStringEx could not be located in the dynamic link library KERNEL32.dll".
After clicking OK, the taskbar has an entry title Cinch Audio Recorder, but the window is solid white. I can close it by right-clicking the taskbar item, and then selecting Close or using Alt-F4.
Running in Compatibility Mode:
Win 95 No error dialog, but have white window only
Win 98 Win Me No error dialog, but have white window only
NT 4.0 Has error dialog and white window only
NT 2000 Has error dialog and white window only
Save | Cancel
We got feedback that the software can't be running on Window XP. We will fix it in the feature. Sorry.
Save | Cancel
The program works fine in recording and separating the tracks. But I too do not receive the ID3 information. The tracks are labelled Tracks1, Track2 etc. I tried the program on two machines both running Windows 10.
From the info on http://cinchsolution.com/ ID3 information should be retrieved in the licensed version. It is unclear from the other comments whether there is a bug or whether this giveawayoftheday is demo software.
Save | Cancel
Bill Rodman,
I can explain it. The time we submitted our software to GOTD is in Feb, but we have updated it in every week since then. Some bugs fixed and some new feature added. By the way, we will update it after this GOTD promotion.
Save | Cancel
Henrik,
Now I understand. It would be cool to try an updated version. Is that possible?
Save | Cancel
I DL'd it and it was missing a DLL. After several attempts I gave up
Save | Cancel
.
Microsoft Media Player did not recognize the tracks, I had to highlight them in Windows Explorer and hit [ Enter ] to get them to play, then they came up in Windows Media Player, but of course, with no identification ...
... then OMG, Microsoft is identifying them, and bring in the album covers!
Okay, I'm sold.
This will allow me to time-shift and sample Pandora with song identification when I'm off-line.
Thanks, Henrik.
Good job, even if you depend on Microsoft a little bit too much.
.
Save | Cancel
.
Interesting, shows promise, but ...
... first computer had all sorts of errors and never got more than half a minute of whatever, buffer too small error, memory error, unable to help identify the problem : poor internet reliability, wandering between 2 to 30 at fast.com, I was torrenting in the background.
Second computer rated a consistent 88 at fast.com, and, doing nothing but Pandora and this software, this software did download 18 songs in 65 minutes before Pandora timed out, but this software could not identify any of the songs, and crapped out with an insufficient buffer message.
"Get ID3 failed" on all, so, how do you get the songs identified?
If I knew this software wasn't going to identify the songs, I'd have printed the screens as Pandora told me all about the artist and lyrics.
So, I recommend they keep working on this to ( a ) test the environment and not crash, but help us troubleshoot, and ( b ) really identify songs.
Audials will patch together song parts to get rid of voice-overs and cut-offs AND listen to all radio stations itself.
That's the competition.
Oh, and torrenting peer-to-peer via proxy to my own server in Finland.
;-)
.
Save | Cancel
Isn't it supposed to download the ID3 tag and automatically add it to the MP3s it records?
So, all songs that have been recorded off of Pandora are labelled as Track1, Track2, etc--and NO ID3 info added at all. When I float my mouse to the right of the time for each track, I get a tooltip banner that says "Cinch Audio Recorder".
How can I get this to auto download the ID3 info and automatically put that in the MP3 info?
Save | Cancel
James D Robinson,
Sorry! The tooltip doesn't say "Cinch Audio Recorder"! (That was still in my clipboard, when I pasted that in.)
It says "GET ID3 FAILED"--every MP3 song I have tried, it says the same thing. No ID3 info downloaded at all. Again--what am I missing? I thought it was supposed to pull that info automatically, and it was "near 100% accurate"?
Save | Cancel
After app start , I see mesage: "Error in procedure LCMapStringEx in KERNEL32.dll ", and white program window. Instaled on XP SP3 32 bits.
Save | Cancel
.
[ Fermin ],
It seems to need nothing else going on, try no anti virus, one radio station, and this software only, and let us know if it squeezes into your computer.
.
Save | Cancel
Fermin,
I reported the same thing. The supported OS list includes XP, but the procedure LCMapStringEx is used to support Vista and above. they should use LCMapString to support XP. Whether they make the change or not is questionable.
Save | Cancel
"Record high quality music ..." Really?
OK, the music might be high quality but the recording won't be. MP3 is definitely not, Not, NOT high quality.
Probably this software is OK for recording lectures and other voice material.
Save | Cancel
.
[ tarvinmarvin ],
Yesm there's no adjustment or report on bit rate or quality / compression.
.
Save | Cancel
starvinmarvin, MP3 ..IS.. what it is! Don't find many devices playing mammoth wav files. Ac3 probably should have been the default.
Good maybe if you are a apple. If I didn't like chinese chow I just wouldn't go there. And I wouldn't blog about it either.
Save | Cancel
Very impressed by this simple program, which has almost no options (the main one being where you want to save your recordings). Up until now I've used Audacity to record sound playing through my laptop's speakers, but his program installed without problem in less than five minutes, and does a very nice job of detecting silence and automatically splitting tracks and saving them in mp3 format.
Save | Cancel
.
[ DComedian ],
Did it identify any songs for you?
.
Save | Cancel
No it didn't Peter, although if you're downloading an album you can use free programs like the outstanding mp3tag or Picard to help fill in all of the information, both of which are invaluable for those of us who like to tag all our music. MusicBee is an excellent music player which can also help, especially in terms of embedding lyrics into a file. :)
Save | Cancel
The program installed flawlessly on my windows10. I tried it out recording a streaming music station, and so far, it cut the songs where it should, and separated the recordings for me, which I appreciate instead of ending up with a two hour long mash of several audio, it separated them into proper and usable sections for me. I found the program very easy to use, and it did a great job recording. The price point for a program like this is about right. I would definitely recommend this program.
Save | Cancel
.
[ Gail ],
Did ANYONE get song's identified?
I got 18 songs with no ID, and 18 snippets of ~4 seconds each, I guess they're the in between silence cut off.
So, how to identify the songs?
Anyone?
.
Save | Cancel
Peter Blaise,
I had to enter names for the tracks myself. I do not think that the program identifies the songs or tracks, I think you have to edit the tag information and enter it yourself. Also, I did have to uninstall the program, due to an issue with my sound going out entirely and would not work at all on my computer, until I got rid of the program.
Save | Cancel
So what you record has to be already playing. Hm.
And whats with the bar graph thing top centre! Its of no value as its not showing frequency/amplitude but a random pattern. Is this a toy?
Save | Cancel
.
[ Paul ],
You can try replay on whatever song was already playing, but yes, for me, 18 songs and no identifications = toy, not ready for prime time.
AbelsSoft.net and KCSoftwares.com and others have taggers, I'll check something, anything -- what can identify unidentified songs?
Not this.
Even though Pandora had all the song information and identification on screen during the entire recording.
Argh.
.
Save | Cancel
What does CINCH do that Audacity doesn't do....
Save | Cancel
If you want to record songs from Spotify or Deezer for instance (not that I would ever condone such behaviour) this program automatically detects silences and saves the songs (and adverts!) as separate mp3 tracks without any input needed from the user. It doesn't do any automatic tagging though.
Save | Cancel
.
[ DComedian ],
There's nothing wrong or illegal in copying or recording anything that arrives in our homes.
Resale or rebroadcast or redistribution are the prohibited activities.
Didn't you put a cassette deck up to your radio at midnight to record the uninterrupted album off FM years ago, or timeshift Roots?
.
Save | Cancel
Nice, simple, straight forward audio stream recorder.
(Clean on virustotal.com (nice), didn't mess with my browsers (nice))
Having used this: Wish list
1. Resizeable dialog GUI would be a nice feature to have
2. By default the music files are added into files off the root of C
These files should be placed into the directory chosen for the install.
3. In a perfect universe it would also include (dare I say), an internet radio with updatable stations.
I say this because I have given up looking for a nice easy to use RESIZEABLE GUI radio program that doesn't contain malware.
Thanks for a nice stream recorder !
Save | Cancel
Another I've had success with and it includes a scheduler is Aktiv MP3 Recorder.
A bit of a learning curve and on some may raise a false malware flag but works great for me.
Save | Cancel
Just to follow up.
First thing I did was play a youtube Vid and record it but made a mistake in my choice I feel- https://www.youtube.com/watch?v=booKP974B0k
You will immediately note that you are able to do more when listening to the audio alone so thumbs up there. Lol>
Interface is clean - and BLAND with no option but for the 1980's Windows blue colour.
Plays well and is nice and simple. Whilst playing its possible to start a recording almost immediately except it checks with you first. An option would be nice to turn this feature off.
Same goes for playing whilst recording - Option please.
One final addition (For fun and for serious usage) would be to record WHILST playing back.
Karaoke is obvious but an audio message with music in the background could easily be created and that could be nice for Grandma. Just a thought.
Thanks Henrik. Nice simple offering and looking forward to v2.02.
Save | Cancel
Very similar interface to a streaming music recorder given away before Christmas but can't detect the ID3 tags or add covers like that software did (at least in the GAOTD version)
I get a 'buffer too small' warning every time I try to record. Stopping and restarting seems to fix this at the expense of missing the first few seconds of recording there is no obvious way to change the buffer size.
Worst of all, the MP3 are less than 128KBPS (110-116KBPS) which is very low quality these days.
Sorry but I've uninstalled. Audacity can do most of what this software promises at much higher quality
Save | Cancel
Zemana blocks the download and Avast prevents the install so BOTH of these programs need a temp disable (Right click) to enable this software to work.
Not tried this offering out yet but thought I would let peeps know how to install before I do.
It WOULD have been nice to not to have to or, because of the nature of this type of software, to have been warned beforehand.
Save | Cancel
Installed with no problems on Windows 10 64 bit system. Records music and separates tracks but is not able to pick up MP3 tag information
Save | Cancel
VLC does the same and 100 times more in other features.
Save | Cancel
sunny2,
As far as I know, VLC is a free and open source cross-platform multimedia player and framework that plays most multimedia files as well as DVDs, Audio CDs, VCDs, and various streaming protocols.
So, what do you mean does the same as we do?
Save | Cancel
Henrik,
"VLC does the same and 100 times more in other features."
"... So, what do you mean does the same as we do?"
FWIW VLC has long had lots of features that were not as well known, &/or used as much. I would not go as far as sunny2's comment myself, but Googling with the term: "vlc recording" [w/out quotes] gets 582k hits, while "vlc record audio" [w/out quotes] gets 520k.
Save | Cancel
Henrik, you CAN dl media with VLC, besides which, as you point out, one can play pretty much all multi media with uncountable customization options.(eq, depth, subs, etc)
Save | Cancel
Henrik, It can record anything you hear or record anything in the background or record live stream or record audio or video in almost any format you can imagine.
Save | Cancel
sunny2, You are right, the negative votes on your counter are just from uninformed persons.
Save | Cancel
I have recorded some songs from spotify and it works well but without the songs cover image
Save | Cancel
Alex,
We hope we could add that feature. But right we had the copyright issue with the cover-image.
Save | Cancel
.
[ Henrik ],
I'd just like song identification -- 18 Pandora songs in an hour and no information is more frustrating than anything else.
And you save the 4-second blanks?
Just more to cleanup for me.
Argh.
.
Save | Cancel
I can't get it to install. I downloaded it twice. I'm presented with a dialog box titled Giveaway of the day and the message is "Failed to launch the program. I also tried running as administrator when executing the program.
Save | Cancel
Jim,
Please try it again after disabling your antivirus software.
Save | Cancel
Jim, Same thing is happening to me...
Save | Cancel
Jim, I just downloaded it from their website and it installed. Give that a try.
Save | Cancel
Jim, if you happen to use Commodo Firewall, check that the viruscope is not enabled. I discovered this by accident, and (free version at least) doesn't bring up any notice when it's blocking.
Save | Cancel
I was recording from iTunes. It only recorded 7 of the 12 tracks. It missed Tracks 4 and 5 as well as any after Track 9. It did not add ID3 tags nor change the name from Track.
It also in About says Version 1.2.2 not 2.0.1 as shown in the GOTD Giveaway.
I was ready to buy this if it worked but it doesn't seem to.
Thanks
Save | Cancel
Elayne,
That should not happen. We haven't received the similar issue reported by other users. You could download the latest version from our official site and see if you still have the same issue.
Good luck
Henrik
Save | Cancel
Henrik, I was trying to record an Apple Playlist. Is that not handled?
As well I followed your suggestion but now I can't run it beyond 5 songs. Can I reinstall the GAOTD version or is there a way to turn the one I dl into a GAOTD app.
Thanks
Elayne
Save | Cancel
.
[ Henrik ],
Would the copy from your site be functional and free?
.
Save | Cancel
Nice tool but there is a better free solution out there to record audio from ANY SOURCE, with the ability to save your audio files in several formats (MP3, AAC, WAV, MP2, OGG, M4A, WMA and etc..).
http://soft4boost.com/any-audio-record
Save | Cancel
That is a dangaros website, be careful!
Save | Cancel
.
[ Henrik ],
I just downloaded and tested PC Win Booster Free, it passed VirusTotal with no flags, installed, and ran without misbehavior.
I suggest that folks include a specific reference when indicting other websites -- thanks.
.
Save | Cancel
Can you schedule a recording for a specific time and date?
Save | Cancel
Doug,
We don't have such option right now. But we will consider to add it in the next updating. Thank you.
Save | Cancel
Installed on windows 10 and records but without any help file (having looked on the web page) I can't see any buttons that will
1. Muted sound while recording (recording when you are in the library)
2.Edit music file and save it as a ringtone
3.Advertisement removal
4.Also i'm confused about MaxBlankTime and gapTime options.
5.I have no idea if it is registered
None of these are in the settings or the about notes
I can only think the GAOTD offering is not the pro version?
If anyone finds a help page that resolves these issue please post it
Save | Cancel
David Murphy,
1. Muted sound while recording (recording when you are in the library)
You can mute the sound on your computer when you are recording. No need to press any button.
2.Edit music file and save it as a ringtone
There is ring bell icon/button in the right of each song, click it to edit music and as it as a ringtone for your phone.
3.Advertisement removal
NO button operation. When you use a free account on music services such as Spotify(or Rdio) then you will heard the short ads that play every once in a while. Our tool aims to wipe off these annoying ads which also get recorded during a streaming session. In this case, you
We submit our software to GOTD in Feb. and we have updated the software since then. We will update the software again after we gather feedbacks from today's GOTD. Please check our official site for the latest version.
Best
Henrik
Cinch Solutions support
Save | Cancel
Henrik, Thanks thats most helpful
Save | Cancel
Program downloaded & installed with no problems, but there's no indication that it has been registered.
How do I register?/Where do I look to check it HAS been registered?
(The "about" button just shows the name & version of the product.)
Thanks for any assistance you can offer.
Save | Cancel
Glenn Norman,
This is the free version of Cinch audio recorder. So, it is NOT necessary to register, and you can use it for free. You could check our official site and download the latest version with new features. Sure you will find a register option there :-)
Good luck!
Henrik
Cinch Solutions support
Save | Cancel
Are you saying it will only work for one day?
Save | Cancel
Joe Schmoe,
If you like the program, please buy it. You will get lifetime updates.
Save | Cancel
Glenn Norman, I have the same problem it installed but no way to tell if it has been activated and registered. I check About and all it gives is companies name now where is GOTD or my name.
I have closed all antivirus and other programs that might interfere and still same thing. So I'm not sure what the problem is I am using win 10
Save | Cancel
Unable to install. After downloading, and unzipping the file it says software activated, however the software isn't installed. Could you please help
Save | Cancel
Roshan,
After it said the software activated, it should start to install the software. The zip file is packed by GOTD. So we can't help you with that. But you can download it from the official site and contact me if you need a free keycode for a day.
Good luck!
Henrik
Cinch Solutions support
Save | Cancel
Roshan, This is most probably due to antivirus software. It prevents unpacking of the giveaway. Thus you receive a message that the software is activated, but actually it was not unpacked or installed. You need to disable your antivirus software, then install the giveaway.
Save | Cancel
Henrik, I did what you said above, and you sent my request tp GAOTD. They don't have the registration code. Please send me one.
Save | Cancel
Henrik,
I also had this problem, can you send me a keycode as well? Thank you.
Save | Cancel
Only records system audio, what you hear, no microphone. Default output directory "C:/Cinch Solutions/Cinch Audio Recorder", it splits recording by silence by default, and i'm confused about MaxBlankTime and gapTime options.
Save | Cancel
This recorder is designed for recording streaming music, not for the microphone. Here are the key features:
Records stream music and save it as MP3 files separately
Supports manual music ID3 tags editing
MaxBlankTime means automatically split music file when the silence is more than a certain time.
Save | Cancel
ew,
How did you install by default on "C:/Cinch Solutions/Cinch Audio Recorder"'? Remark: Windows paths separators are "\", not forward slashes "/".
On my box it installs in "C:\Program Files" and the setup offers you to install in the directory of your choice.
Save | Cancel
ew,
Please discard my previous comment (my mistake, sorry, I commented before running the program).
The path you refer to is the location of the output folder, which can be changed in "Setting".
Note to the developers
Of course, the default directory for output should be something like "%USERPROFILE%\Music", not the one you mention. And although Windows accepts "/" as path separator, the normal one is "\".
Save | Cancel
Hi,
When you click the software installer, it starts to unpack all necessary files on your computer. You saw the path "C:/Cinch Solutions/Cinch Audio Recorder" on the installer NOT on Windows file explorer. I think it's fine. I have checked other software installers, they have the same way to show the file path.
Save | Cancel
ew,
"Only records system audio, what you hear, no microphone."
Couldn't you un--mute or turn on the feature to monitor mic input? AFAIK the reason the mic input isn't automatically routed to speaker out is the potential for feedback if you're not using headphones, but also AFAIK that's something you normally can turn on.
Save | Cancel
.
[ Henrik ],
MANUAL ID3 tags only?
Then why did it say "Get ID3 failed"?
I thought it was supposed to identify the songs.
If not, it's just a streaming voice/silence-activated stream-recorder, right?
.
Save | Cancel
mike, yes, i could, thanks.
Save | Cancel
Henrik, thanks for your answers.
Save | Cancel
papin, i copied that path with / from the options window, just didn't pay attention to /.
Save | Cancel
Works like a charm! Now I don't have to listen to the same children's music CD over and over again in my car. Thanks!
Save | Cancel