English
Every day we offer FREE licensed software you’d have to buy otherwise.
$24.99
EXPIRED
Giveaway of the day — AudioGrail 7.9.0
The swiss army knife for everything that is related to audio files.
$24.99
EXPIRED
User rating:
98
61 comments
AudioGrail 7.9.0 was available as a giveaway on January 28, 2017!
Today Giveaway of the Day
Let BeeConverter endow your video with vitality!
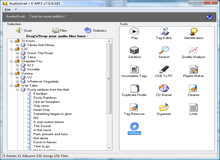
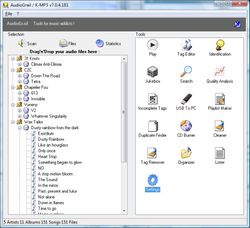
AudioGrail (Formerly K-MP3) is the best solution to work with audiofiles, such as MP3, OGG, MPC etc. Rename and tag your files (add artist name, album, title etc.) automatically. The program can organize files on your system, analyse their quality, find duplicates and improve your audio experience.
Key Features:
- Supports MP3, OGG, MPC, APE, AAC, FLAC, WavPack files, ID3Tag V1 and V2 tags, Vorbis (Ogg) comments and APEv2 tags;
- Automatic Album renaming, Song identification, Album covers finding and Tagging;
- One-by-one tag editor with queue (for multiple files edition);
- Audio files To Audio CD burning capabilities (requires CopyToDVD);
- File Names and Tags Normalizer (Case Standardization), Mass Tags Remover;
- Files Organizer, Duplicate Files Finder;
- Playlist Creator and Analyser (supported formats: m3u, pls, xpl);
- Files Lister (supported formats: Raw listing, Coma Separated Values, SQL, XML);
- Incomplete Tags Finder;
- Quality Analyser and more!
System Requirements:
Windows NT/ 98/ Me/ 2000/ XP/ 2003/ Vista/ 2008/ 7/ 8/ 10; 128 MB RAM
Publisher:
KC SoftwaresHomepage:
http://www.kcsoftwares.com/?kmp3File Size:
1.9 MB
Price:
$24.99
How would you improve AudioGrail 7.9.0?
GIVEAWAY download basket
Developed by Informer Technologies, Inc.
Heal up your system and speed up your PC with the help of 25.
Developed by IObit
Developed by OmicronLab
Comments on AudioGrail 7.9.0
Thank you for voting!
Please add a comment explaining the reason behind your vote.
Please add a comment explaining the reason behind your vote.
You can also add comment viaFacebook
Facebook comments
iPhone app giveaways »
$1.99 ➞ free today
This app is an autistic person's dream. It's like your favorite screensavers but interactive.
$0.99 ➞ free today
$0.99 ➞ free today
SAND is a powerful grid-based sequencer designed to create music using plugins and external MIDI devices.
$9.99 ➞ free today
For those of us who can appreciate weird and funny drawings, these stickers can’t fail to fascinate.
$0.99 ➞ free today
Android app giveaways »
$43.99 ➞ free today
$2.99 ➞ free today
$2.49 ➞ free today
$0.99 ➞ free today
Blur Photo is the perfect censor photo app for blur background and picture blur.
$2.99 ➞ free today


You have some Duplicate Files on your computer which hampers your memory space.
Just use "DuplicateFilesDeleter".If you use this software you will be get comfortable.
Save | Cancel
I actually like much of KC Software's offerings, but AudioGrail just has never held a candle to the freeware Mp3Tag.
Save | Cancel
With all due respect, a "meh" group of utilities--individual sources from elsewhere seems preferable. And the album art fetcher process, the reason I wanted this software, is not an automatic process. Perhaps fine to have around and sometimes use, as a secondary source.
Save | Cancel
Mike S., The art fetcher with iTunes is quite good
Save | Cancel
I downloaded and installed the program without any problems. It did leave me with 3 links which I checked out and deleted as they were of no concern. The program does as it claims and I have no errors as of yet so I am OK with it. It is a good program and given a proper chance it will perform as expected. If not I will uninstall, but only after I check it fully.
We should be a little more grateful for GOTD and show some respect for their hard work. Stop being so disrespectful to them and their patrons. No one is perfect and I expect a few drawbacks. I am a retired software teacher and installer since 1985 so I do have a little knowledge of the computer.
We have a good thing here so lighten up. Thank you GOTD and all of your participants.
Save | Cancel
I tried this mainly for its claimed ability to add album covers. "•Automatic Album renaming, Song identification, Album covers finding and Tagging" After using for an hour there appears no way to find and add album covers. So fo me it's just another organizer.
Save | Cancel
It would be nice to read a comment on the effectiveness of the software, if one decided to install it after all the paranoia. How does it work for the purpose intended? IS it a good tool for working with audio files?
Save | Cancel
The developer has the audacity to put web links on your desktop without your permission.
Sumo is hardwired into the EXE file so if you delete the icon it will reappear again.
Because of this disgraceful behaviour I uninstall the program and will have nothing to do with this company programs in the future.
Save | Cancel
XP-Man,
Very clever! 'audacity' better alternative.
Save | Cancel
MP3 Tag Express blows this out of the water in terms of what it can do, but unfortunately it doesn't have the auto-lookup tags for files themselves, just audio discs. It also costs money.
Save | Cancel
George Taylor, Hey great and well written review of THIS product.... NOT!
Save | Cancel
Does anyone know if this will batch normalize the volumes?
Save | Cancel
Will someone please talk about the merits of diadvantages of the software and stop attacking each other.
Save | Cancel
NOTHING got installed on my system without my permission the only thing they did and below whiners neglected to check are 3 weblinks to another software. That said, this is a great piece of software and works as advertised
Save | Cancel
Mavadelo, p.s I install with an install monitor that keeps track of anything that get's installed on my system and this CONFIRMED only Audiograil was installed and NOTHING ELSE
Save | Cancel
Mavadelo, do you work for KCSoftwares who just pretend to be an innocent user?
Save | Cancel
Berry1, you must be new to this site or else you would know I am a regular and not working for any developer
Save | Cancel
Berry1 are you are a troll? I will think yes! Please stay away from this site!!!
Save | Cancel
nibo1978, way to be mature. NOT!!!!
Save | Cancel
"FREE"... there's always strings attached ...
I'll stay with TagScanner for working with MP3 tags (http://www.xdlab.ru/en/download.htm) So far it's the BEST MP3-tagger I've found. OK, it's ".ru" (Russia) but I use it for maaaany years, and never had any problem, no ads, no spyware, just a very good program...
Save | Cancel
Be careful......associated CRAP without consent during installation !!!
Save | Cancel
jan, nope just 3 weblinks that can be dragged to trash and you are done
Save | Cancel
Mavadelo, I looked into their software with HEX editor, they have hard wired links to other web sites that can not be dragged into the trash folder. Legitimate concern still remains after the deletion of the 3 icons.
Save | Cancel
Berry1, I did the same and actually looked at what the links are for. most of the "hardwired" links are going to the KCsoftware sites to check if your software is legit, to register, to help files and such. Some of the other links are used for the unregistered version of the software to redirect you to a place to buy, other links are needed to be able to find the tags. Again.. assumptions assumptions. Did you even read the description of the software and know what it can do? you think it will find missing tags and info just by magic alone? No you probably noticed weblinks, didn't bother to check out what these weblinks are connected to and found validity for your paranoia
Save | Cancel
jan, it install no crap this are only weblinks to their other products. Must software developer install weblinks to their other products!
Save | Cancel
Mavadelo, Thank you. This is what this site is SUPPOSED to be about. I feel very confident in looking into this software now. I wish others would put in a little effort to actually test and review software so the rest of us can read and make an informed decision.
Save | Cancel
With all due respect, Ian and Richard, I don't see what you're talking about.
I installed it on a Windows 8.1 system, and I got one piece of software. I read the terms and conditions carefully to be sure I didn't need to "opt out" of installing anything. The user interface does show about 16 different options on the right-hand side, but that is shown in the screenshots and also in the description at Software.Informer (if you visit their website to do a little extra research before installing):
AudioGrail offers you a collection of 15 audio utilities to help you organize, store, and distribute your MP3 files and other compressed-audio formats, both lossy and lossless – OGG, MPC, APE, AAC, FLAC and WavPack. AudioGrail renames, tags, normalize names, creates playlists and even burn your audio CDs in an intuitive and simple way.
So there are no extra programs you didn't ask for from what I can see.
Save | Cancel
All KC Softwares giveaways on GOTD are full of crapware because GOTD don't point you to the Lite installer which contains no junk.
http://www.kcsoftwares.com/files/audiograil_lite.exe
Works with the license in the readme.
Save | Cancel
Jeff Dalls, but the lite version has a limit on the number of files, right?
Save | Cancel
Thanks, Ian. Sorry AudioGrail but my improvement recommendation would be to offer a "CLEAN" install if you want your software tested.
Save | Cancel
I have yet to find an app that "automatically" tags and downloads album art, even though many claim to. Like all the others, you have to click through a process. "Semi Automatic" at best. Unfortunately, this app fails to download album art, and returns "Errur Jpeg 42".
Save | Cancel
WTF this downloaded other crap on to my PC without any prior warning and more importantly without my permission. Totally unacceptable. GOTD's quality and standards have slipped very badly over the past months but for me this was the last straw. I'm never going to use this site again and will block it from being accessed on all my PC's there are much better and more reliable sites that I will continue to use in the future. GOTD you really need to pick up your game if you want to remain in business, the way you are going hopefully we'll read of your demise before very long.
Save | Cancel
GOTD_nomore, this are only weblinks to other products from KCSoftwares. Other developer do the same.
Save | Cancel
Is there a way to remove the JUNK UNINVITED software that automatically installs itself without authorization?
Save | Cancel
Richard Hind, yes you can drag the 3 WEBLINKS to the trashcan and you are done
Save | Cancel
Richard, did you happen to notice what the junk was called?
Save | Cancel
Julia, Dumo, Sumo and Kcleaner and they are just weblinks. nothing got installed without authorization, people just fail to look. they see 3 icons and ASSUME something without checking it.
asumptions are the mother of all F ups
Save | Cancel
Richard Hind, no indication at all that it is going to install any 'extras' so I took note of what everyone said and didn't install it. If you try Revo Uninstaller (free - scroll down below past the paid version http://www.revouninstaller.com/revo_uninstaller_free_download.html) you can order installations by date, which should help identify anything installed today. I am sure many people on here have a copy of Revo on their computers...
Save | Cancel
The comments about the weblinks weren't there when I was typing - so I will give it a go. Still Revo is useful to check such things... :)
Save | Cancel
Mavadelo,
Links were installed without authorisation!
This is totally unacceptable behaviour by a developer, Sumo is hardwired in the EXE.
Removed the link from my desktop only for it to reappear again.
Uninstalling program.
Save | Cancel
XP-Man, Hi xp-man, if you are the "real xp-man" (i can't check obviously) I give you some more credit than the "average visitor" knowing your posts in the past. I have restarted both the program and my system several times to try and reproduce your experience but wasn't able to. After initial deletion of the icons it stayed away.
As for unacceptable, I kinda agree they shouldn't do it but then... this is a giveaway so I don't blame them. Would you care to enlighten me what the circumstances were that made them resturn soI can try that myself as well :)
Save | Cancel
xp-man, I found one Sumo reference at 12AC14 which was not a hyperlink, I did not find references to the other two
Save | Cancel
Mavadelo, Yep, I checked if it was installed as seperate programs, found none, so assumed it was an integral part of the main program. Thanks to you and all those that replied.
Save | Cancel
Rae Perez, Thanks for replying, and it appears not to be installations, but merely Web Page Icons. Going to check the registry to see if there's anything hiding!
Save | Cancel
Mavadelo,
I can assure you that I am the original XP-Man; took time out as at 74 my body dictated my circumstances.
I cleared the icon from my desktop but on restarting it reappeared.
Search within the programs download folder for Sumo and there it was in the EXE file.
To be honest my desktop is a mess but I have it under control as long as unnecessary icons don't just appear.
In my opinion developers should request permission when installing anything other than the program anticipated, today's developer failed miserably.
Save | Cancel
question if you install a software that is free on that day and you need to wipe windows and start again sometime and want to reinstall a software you give us some time past will the key still work?
Save | Cancel
Stephen, in general no, exceptions are there. Ashampoo software if you manage to keep the GOTD installer (find the key on your ashampoo account) is one of those
Save | Cancel
Stephen, No it will not work
Save | Cancel
Stephen, No.
Save | Cancel
hi
Thanks yes that's a point so some you can but mostly no
Save | Cancel